Cluster Resampler

This notebook shows how clusterResampler methods are used to create synthetic samples. clusterResampler relies on a Python package k-means-constrained to cluster the data. There are two methods demonstrated in this notebook. The first one draws synthetic values from a multivariate normal distribution. The second one draws synthetic values from a gaussian copula.

from synloc import sample_circulars_xy, clusterCov, clusterGaussCopula

Data

df = sample_circulars_xy(1000)
df.head()

	x	y
0	-7.439214	-6.410053
1	-16.626527	-10.295054
2	6.669369	19.920039
3	16.274841	5.968006
4	7.181718	-2.006049

Using Multivariate Normal Distribution

We use clusterCov method to create synthetic data. There are three crucial parameters to define the cluster properties. The first one is the number of clusters, n_cluster. The second and the third ones are the required minimum and maximum cluster sizes respectively. The second and the third ones are optional, however, it is advised to consider the the required minimum cluster size while choosing the resampling method.

syn_cov = clusterCov(df, n_clusters=20, size_min=10)
syn_cov.fit()

	x	y
0	-10.447402	7.088786
1	-4.048904	15.440417
2	-8.741493	9.510548
3	-7.061347	14.254181
4	-5.263386	16.549055
...	...	...
31	-6.509278	-25.342745
32	-4.047308	-21.856602
33	-3.537834	-23.911015
34	-4.728510	-21.240394
35	-3.581509	-24.209864

1000 rows × 2 columns

syn_cov.comparePlots(['x', 'y'])

Using Gaussian Copula

syn_cop = clusterGaussCopula(df, n_clusters=20, size_min=10)
syn_cop.fit()

	x	y
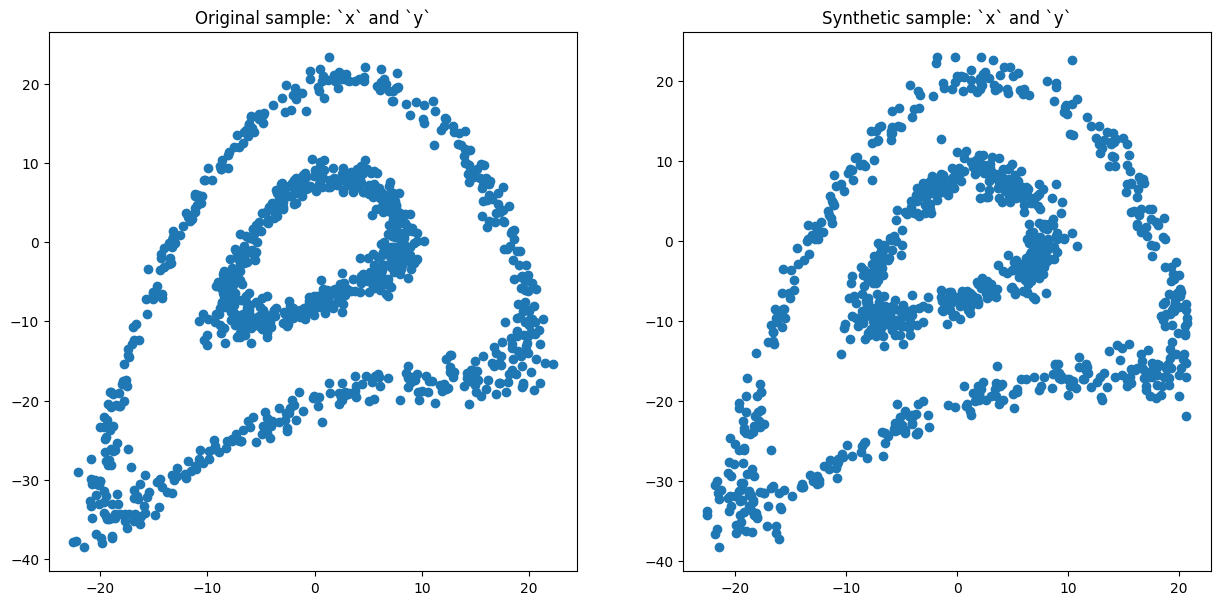
0	0.705895	21.506721
1	7.240778	20.261066
2	5.910154	21.063820
3	6.170739	20.511732
4	0.763095	21.702028
...	...	...
33	2.251692	-17.754208
34	3.807215	-18.830935
35	2.790674	-21.364349
36	0.264260	-19.779841
37	-1.980704	-20.683878

1000 rows × 2 columns

syn_cop.comparePlots(['x', 'y'])